Les coordonnées

Il peut s'avérer utile pour certaines figures de connaître la position de la tortue. Cependant, l'exemple de la sphère montre qu'il existe parfois des manières très différentes de repérer un point, en l'occurence grâce au couple latitude/longitude ou par ses coordonnées dans un repère de l'espace à trois dimensions.

Puisqu'il existe plusieurs façons de repérer un point, il a fallu faire des choix. GéoTortue propose ainsi un éventail de fonctions coordonnées qui prennent toutes en argument le nom ou le numéro d'une tortue. Selon le cas, certaines coordonnées sont celles intrinsèques de la géométrie considérée, tandis que d'autres se réfèrent à l'espace graphique, qui joue le rôle d'espace ambiant dans lequel la géométrie est plongée.

Par ailleurs, une fonction permet de calculer la distance intrinsèque entre deux tortues (voir en bas de page).

L'espace graphique

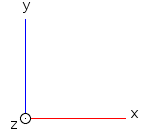
Il s'agit de bien distinguer l'espace abstrait dans lequel évolue la tortue et sa projection sur l'écran (l'espace graphique). Dans sa configuration initiale (c'est-à-dire avant toute manipulation à l'aide de la souris), l'espace graphique est orienté selon un repère (Oxyz) tel que l'origine O se situe au centre de l'écran et l'axe des z pointe vers l'utilisateur perpendiculairement à l'écran, comme illustré sur la figure ci-dessous.

Géométrie euclidienne à 2 ou 3 dimensions

C'est le plus simple des cas : les coordonnées de la géométrie coïncident avec celles de l'espace graphique.

Fonction	Coordonnée
X	Abscisse
Y	Ordonnée
Z	Cote

La fonction Z n'est bien entendu disponible que dans le cas de la géométrie à 3 dimensions.

Exemple

av 200 ; td 90 ; av 100
aff X(Achille) Y(Achille)

Géométrie sphérique

En plus des coordonnées de l'espace graphique, deux fonctions renvoient la longitude et la latitude exprimées en radians. Dans la configuration initiale de l'espace graphique, l'équateur (latitude nulle) correspond au plan y=0 tandis que le méridien de référence (longitude nulle) correspond au plan x=0.

Fonction	Coordonnée
U	Latitude en radians
V	Longitude en radians
X	Abscisse dans l'espace graphique
Y	Ordonnée dans l'espace graphique
Z	Cote dans l'espace graphique

Exemple

av 50; td 90; av 50
aff X(Achille) Y(Achille) Z(Achille)
aff U(Achille) V(Achille)
à Bénédicte; tlp U(Achille) V(Achille)

Demi-plan de Poincaré

Avertissement : je suis bien conscient que les explications ci-dessous sont laconiques, le sujet réclamant des connaissances de géométrie qui ne peuvent être résumées en quelques lignes.
Par ailleurs, je ne sais pas s'il existe un jeu de coordonnées plus naturel qu'un autre : toute remarque à ce sujet est la bienvenue.

Les calculs en géométrie hyperbolique dépassent rapidement les limites de précision (à cause notamment de la présence du cosinus hyperbolique dans l'expression des distances - cf. le calcul en virgule flottante). Par conséquent, le choix d'un système de coordonnées suffisamment stable s'est avèré délicat. Loin d'être idéales, les coordonnées sur l'hyperboloïde semblent néanmoins présenter quelques avantages, et c'est la raison pour laquelle elles figurent dans les formules de projection.

L'hyperboloïde de référence est la surface définie par

et munie de la distance :

Le demi-plan de Poincaré est un modèle de géométrie hyperbolique qui se déduit de celui de l'hyperboloide par l'application

dont la réciproque s'écrit :

Fonction	Coordonnée
U1	Coordonnée xH
U2	Coordonnée yH
U3	Coordonnée zH
X	Abscisse dans l'espace graphique (X = s × rayon)
Y	Ordonnée dans l'espace graphique (Y = t × rayon)

Exemple

av 50; td 90; av 50
aff U1(Achille) U2(Achille) U3(Achille)
aff X(Achille) Y(Achille)
à Bénédicte; tlp X(Achille) Y(Achille)

Disque de Poincaré

Le disque de Poincaré est un modèle de géométrie hyperbolique qui se déduit de celui de l'hyperboloide par l'application

dont la réciproque s'écrit :

Fonction	Coordonnée
U1	Coordonnée xH
U2	Coordonnée yH
U3	Coordonnée zH
X	Abscisse dans l'espace graphique (X = s × rayon)
Y	Ordonnée dans l'espace graphique (Y = t × rayon)

Exemple

av 50; td 90; av 50
aff U1(Achille) U2(Achille) U3(Achille)
aff X(Achille) Y(Achille)
à Bénédicte; tlp X(Achille) Y(Achille)

Géométrie à quatre dimensions

Fonction	Coordonnée
X1	Première coordonnée x1
X2	Seconde coordonnée x2
X3	Troisième coordonnée x3
X4	Quatrième coordonnée x4
X	Abscisse dans l'espace graphique
Y	Ordonnée dans l'espace graphique
Z	Cote dans l'espace graphique

Exemple

tlp 10 20 30 40
aff X1(Achille) X2(Achille) X3(Achille) X4(Achille)
aff X(Achille) Y(Achille) Z(Achille)
mg rotation yz 90
aff X(Achille) Y(Achille) Z(Achille)

Distance entre deux tortues

Si t1 et t2 désignent deux tortues (par leur nom ou leur numéro), l'expression dist(t1 , t2) renvoie la distance les séparant dans la géométrie considérée.

Exemple : quelque soit la géométrie, les commandes ci-dessous permettent de tracer un triangle rectangle isocèle.

à Achille ; av 100; td 90; av 100
à Bénédicte; vise Achille; av dist(Achille, Bénédicte)