Le demi-plan de Poincaré

Il s'agit d'un modèle de géométrie hyperbolique imaginé par Beltrami et nommé en l'honneur de Poincaré qui l'a intensivement exploité et popularisé. Il est construit à partir du demi-plan constitué des points dont l'ordonnée est strictement positive. La façon de mesurer les distances y est en revanche très différente.

Un pavage du demi-plan de Poincaré par des pentagones réguliers

Géodésiques

Le chemin le plus court entre deux points est soit un segment de droite (euclidienne) perpendiculaire à l'axe des abscisses, soit un arc de cercle (euclidien) dont le centre est situé sur l'axe des abscisses.

Les droites en bleue sont toutes parallèles à la droite en rouge

Options

Le « rayon » du demi-plan est un scalaire positif qui joue un rôle analogue au rayon d'une sphère. En particulier, la courbure du demi-plan de Poincaré vaut

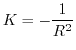
tandis que la courbure d'une sphère s'écrit

En pratique, on choisit souvent l'unité pour le rayon afin de simplifier les calculs.

La « rotation hyperbolique » a pour effet de faire « tourner » le demi-plan autour de son « centre ». Plus précisément, il s'agit d'une rotation de l'hyperboloïde autour de son axe avant sa projection sur le demi-plan de Poincaré .