Introduction : euclidien ou non-euclidien ?

La géométrie d'Euclide

La géométrie à laquelle chacun est habitué, celle étudiée au collège et au lycée, s'appuie notamment sur un postulat simple, appelé cinquième postulat d'Euclide : étant donnés une droite d et un point A extérieur à celle-ci, il existe une seule droite parallèle à d passant par A.

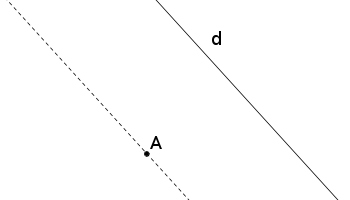
Ce postulat est par ailleurs équivalent au fait que la somme (des mesures) des angles d'un triangle vaut 180°.

Postulat ou théorème ?

Depuis que Euclide a rédigé ses Éléments, qui compilent en particulier les fondements de la géométrie, le cinquième postulat semblait trop « évident » ou « intuitivement vrai » pour constituer un postulat (un principe posé comme fondement). C'est pourquoi, à travers les âges, de nombreux savants se sont acharnés à prouver qu'il ne pouvait en être autrement : le cinquième postulat devait être un théorème, déduit des autres hypothèses de base.

Il faudra attendre le XIXème siècle et les travaux d'illustres mathématiciens (notamment Bolyai, Lobatchevski, Gauss, puis Riemann, Beltrami, Klein, Poincaré parmi les plus célèbres) pour se rendre compte que la quête, qui aura duré plus de deux mille ans, était vaine : il existe des géométries, dites non-euclidiennes, qui sont tout à fait cohérentes et répondent à toutes les exigences de la géométrie euclidienne, à l'exception du cinquième postulat.

Comment est-ce possible ?

Pour illustrer la possibilité de telles géométries, c'est à dire n'obéissant pas au cinquième postulat, supposons qu'un explorateur imaginaire effectue en montgolfière le périple suivant : décollant d'un lieu situé sur l'équateur, il rallie le pôle nord, puis modifie sa direction en effectuant un quart de tour vers sa droite et voyage jusqu'à l'équateur ; une fois arrivé, il lui faut désormais suivre l'équateur pour retourner à son point de départ, et donc tourner d'un quart de tour vers sa droite ; enfin, s'il voulait repartir en direction du pôle nord, il lui faudrait une fois encore tourner d'un quart de tour à droite.

Il est très simple d'utiliser Géotortue pour simuler ce voyage : une fois la géométrie sphérique sélectionnée dans les préférences, il suffit de saisir la ligne de commande suivante (le rayon de la sphère supposé égal à 100) :

rep 3 [ av 50*π ; td 90 ]

Le « triangle » ainsi obtenu est équilatéral, de côté 50π, et possède trois angles droits, ce qui contredit clairement le cinquième postulat.

L'objection naturelle que l'on peut formuler est bien entendu que les côtés de ce triangle ne sont pas des segments de droite. Pourtant, pour un être contraint à évoluer sur la surface de la sphère, ces arcs de cercle constituent bel et bien les plus courts chemins entre leurs extrémités (on dit que ce sont des géodésiques), et satisfont par conséquent à la définition de segment de droite.

Ces nouvelles géométries exigent donc de renoncer à notre conception euclidienne du monde, en autorisant des lignes droites qui apparaîtraient courbes pour un observateur extérieur.

Classification des géométries non-euclidiennes

L'exemple du triangle sphérique dont la somme des angles vaut 270° est loin d'être une exception. C'est en fait la règle pour tous les triangles que l'on peut tracer sur la sphère : la somme de leurs angles est toujours supérieure à 180°. Une telle géométrie, pour laquelle deux droites distinctes sont par ailleurs toujours sécantes, est dite elliptique.

A contrario, il existe des géométries pour lesquelles la somme des angles de tout triangle est inférieure à 180° : ces géométries sont dites hyperboliques. De manière équivalente, par un point extérieur à une droite passe une infinité de parallèles. La figure ci-dessous montre un exemple de pavage du demi-plan de Poincaré (un modèle de géométrie hyperbolique) par des triangles équilatéraux.

La notion fondamentale (mais difficile) sous-jacente est celle de courbure, dont la paternité revient à l'éminent mathématicien Gauss. Sans entrer dans trop de détails, notons simplement que la classification ci-dessus s'exprime en des termes simples à l'aide de la courbure : pour les modèles ci-dessus, elle est constante, positive dans le cas elliptique, négative dans le cas hyperbolique, et nulle pour la géométrie euclidienne.

Ajoutons en outre que certaines surfaces, comme par exemple le tore de révolution, présentent en quelque sorte des propriétés mixtes : la courbure n'y est pas la même partout, tantôt positive, tantôt négative selon le point considéré. Un théorème affirme néanmoins que les géométries à courbure constante sont les plus « intéressantes », au sens où elles sont les plus riches en symétries (isométries).

À ceux qui ne sont pas convaincus...

L'étude de ces géométries a priori exotiques peut sembler n'être au premier abord qu'un sujet purement mathématique, dénué d'intérêt pour le non-spécialiste. Sans évoquer les nombreuses applications scientifiques et technologiques de ces géométries, ni le rôle fondamental qu'elles jouent dans la quasi-totalité des mathématiques actuelles, nous soutenons pourtant la thèse que leur simple existence, certes abstraite, justifie à elle seule que l'on s'y intéresse.

Il faut néanmoins reconnaître que le cas non-euclidien est par bien des aspects déroutant, car notre intuition, construite sur les principes d'Euclide, n'est souvent d'aucune utilité, au contraire. Il s'agit dès lors d'acquérir de nouveaux automatismes, fondés sur des images mentales différentes de celles auxquelles la géométrie euclidienne nous a habitués.

En guise d'illustration, et pour citer un écueil typique des géométries non-euclidiennes, considérons le triangle équilatéral. Pour Euclide, il est clair que l'un quelconque de ses angles mesure 60°, quelque soit la longueur de son côté. Il en va d'une toute autre manière pour les géométries hyperboliques ou elliptiques : la mesure commune aux angles d'un tel triangle dépend cruellement de la longueur du côté ! Le piège étant qu'en outre, pour de petites valeurs du côté, les angles sont presque égaux à 60° (pensez à la Terre et aux lignes qui nous semblent droites à sa surface).

Pour conclure, il nous semble important que nos élèves entendent parler un jour de géométrie sphérique (au moins) et qu'ils appréhendent ainsi la singularité de ces géométries : qu'ils se convainquent par exemple que la distance entre Paris et New-York ne peut se mesurer sur une carte (et encore moins à l'aide du théorème de Pythagore), qu'il existe des triangles dont la somme des angles atteint 270°, et plus largement que les mathématiques, loin d'être un carcan, ouvrent au contraire les esprits et l'imagination à des possibilités insoupçonnées.