Aide en ligne » Les géométries » Les quotients du plan
Quotients rectangulaires du plan
Derrière ce nom compliqué se cache une idée très simple : contraindre la tortue à évoluer dans un rectangle. Pour celà, il suffit de recoller les bords de ce dernier comme l'illustre l'animation ci-dessous.
Une « droite » sur le tore
L'idée de cette géométrie un tantinet exotique vient des premiers logiciels exploitant le langage Logo : la tortue ne devant pas sortir du cadre, elle réaparaissait de l' « autre côté ». Nous n'avons pas manqué cette occasion pour discuter un peu de topologie.
Recollements
Pour le lecteur débutant, cet article de vulgarisation, rédigé à l'occasion de la démonstration de la conjecture Poincaré par le mathématicien russe Grigori Perelman, propose une introduction à la topologie et aux objets décrits ci-dessous.
Il existe en effet plusieurs façons de recoller les bords d'un rectangle : la manière peut-être la plus naturelle consiste simplement à identifier les côtés opposés selon le plan de montage suivant. Topologiquement parlant, on obtient par cette méthode un objet semblable (homéomorphe) à un tore (plat).
Si deux seulement des bords sont recollés, c'est un cylindre :
Les choses commencent à se compliquer un peu lorsque l'on considère l'orientation : ainsi est-il possible de faire coïncider deux côtés d'un rectangle en effectuant au préalable un demi-tour, schématisé par des flèches de sens opposés. On élabore de cette façon le célèbre ruban de Möbius.
En poussant le jeu plus loin, il est possible de construire la non moins célèbre bouteille de Klein.
La difficulté à visualiser cet objet vient du fait qu'il n'est pas possible de le plonger dans l'espace à trois dimensions : les intersections sont fictives, comme expliqué dans l'article de vulgarisation cité plus haut.
Enfin, la dernière combinaison fournit un objet encore plus délicat à visualiser en trois dimensions : le plan projectif réel. L'illustration choisie est la surface de Boy.
Précisons que pour toutes ces géométries la courbure est nulle (la somme des angles d'un triangle vaut 180°). Cela ne contredit en rien le fait que par exemple la courbure d'un tore de révolution est en général non-nulle, car il ne s'agit pas de la même métrique. En d'autres termes, un homémorphisme ne conserve pas nécessairement la courbure.
Géodésiques
Le chemin le plus court entre deux points est un segment de droite (euclidienne) ou la réunion de tels segments.
Options
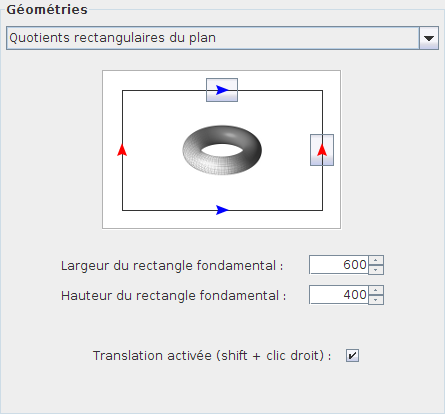
Les boutons contenant les flèches bleues et rouges permettent de choisir le type de recollement des côtés du rectangle.
Les dimensions du rectangle sont ajustables à l'aide des compteurs.
La « translation » consiste à déplacer le plan avant projection sur le rectangle. L'animation ci-dessous illustre le phénomène dans le plan projectif.
Le flocon de Von Koch dans le plan projectif...






